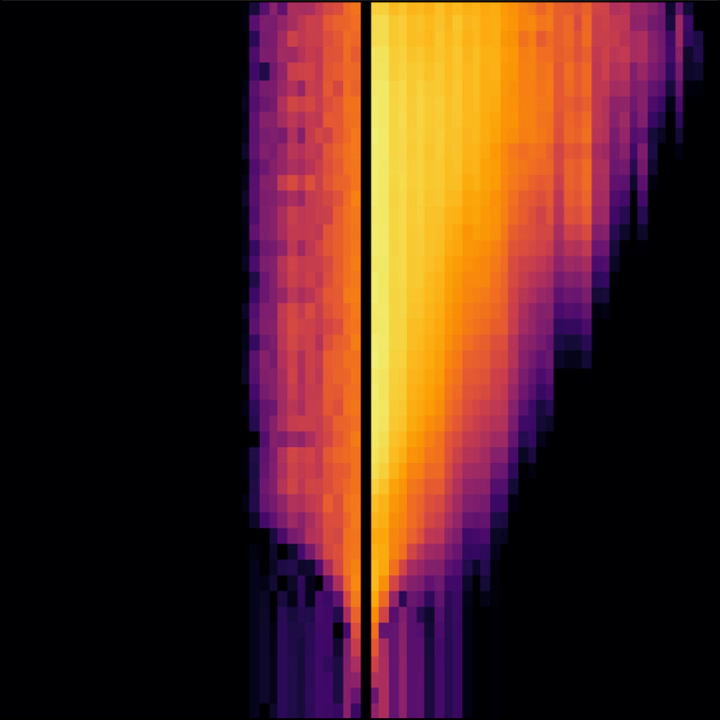
앤더슨 국소화 시스템 (왼쪽)에 비해, 다체 국소화 시스템(오른쪽) 은 양자적 상광함수가 무기적으로 확산됩니다. 이 현상은 Out-of-Time-Ordered-Correlator로 시각화 할수 있고, 1차원과 2차원 보손들에 대해서 시뮬레이션 되었습니다. x축은 공간이고 y축은 로그시간입니다.
일반적인 사람들을 위해 (클릭해 열고 닫을수 있습니다)
커피믹스와 우유를 컵에 넣으면, 우린 보통 두가지의 입자들이 섞여, 라떼라는 균질한 혼합상태가 될거라고 생각합니다. 물리학자들은 이런 현상을 보고 시스템이 ‘열평형화’(thermalization) 된다고 표현합니다. 컵과 우유 뿐만아니라, 많은 일반적인 상황에서, 우린 감각적으로 시스템들이 열평형상태로 도달할거라고 예상합니다. 여기서 ‘시스템’ 이란, 위의 예의 유체 물리같은 어떤 ‘법칙’과, 커피 믹스와 우유 입자들 같이 그 법칙을 따르는 대상들의 집합을 뜻합니다.
하지만 열평형화가 되지 않는 시스템들도 존재합니다. 입자간 아무런 소통을 하지 않는 ‘비상호작용’ 시스템들은 입자간 섞일수 없기 때문입니다. 물리학자들이 중요하게 생각하는 비상호작용 시스템중, 중요하게 여겨지는 ‘앤더슨 국소화’ (Anderson Localized)되어 있는 시스템들이 있습니다. 입자들이 초기 상태에서 멀리 퍼지지 않고 한곳에 모여있기때문에 ‘국소화’ 되어 있다고 표현합니다. 이 현상을 다른 관점으로 생각해 보면 해석해 보면, 초기 상태의 기억을 잃지 않는다고 해석할수 있겠죠.
순진하게 생각해 보면, 우리는 상호작용을 하는 시스템들은 모조리 다 열평형화 될꺼라고 생각할수 있습니다. 하지만, 예상과 다르게 특정 상황에선 상호작용을 하는 시스템마저 국소화되어, 열평형상태가 되지 않는 경우가 있습니다. 이런 시스템들을 ‘다체 국소화’ (Many-Body Localized, MBL) 시스템이라고 하고, 다체 국소화(MBL)는 오늘날 응집물질물리 연구에 중요한 분야중 하나입니다. 이론 물리학자들은 보통 이런 현상을 ‘격자’ (lattice)에서 공부합니다. 격자란 공간을 단순화 한것으로, 입자들이 연속적인 위치에 존재하는것이 아니라, 이산된 ‘자리’에 위치 한다고 단순화 하며, 각 위치가 분리되어 있는 상태라고 생각하는 것입니다.
물리학에는, 두가지의 기초적 입자들이 존재합니다. 첫번째는 ‘페르미온’ 이라는 입자 인데, 한 자리에 최대 한개의 입자가 자리잡을수 있다는것이 특징입니다. 두번째론 ‘보손’ 이라는 입자가 있습니다. 보손은 한 자리에 자리잡을수 있는 입자의 갯수가 제한되어 있지 않습니다. 최근, 실험물리학자들은 다체 국소화 (MBL) 시스템들을 보손입자를 이용하여 공부하고 있습니다. 그런데, 이론적으로나 연산적으로나, 페르미온에 비해, 보손을 공부하는것이 훨씬 더 어렵습니다. 왜냐고요? 우선 페르미온이 가질수 있는 상태를 모두 고려해봅시다. 각 자리에 페르미온이 있을수도, 없을수도 있기때문에, $2 \times 2 \times \cdots \times 2 = 2^L$ 가지의 경우의 수가 있습니다 (여기서 $L$는 자리의 총 갯수를 뜻합니다). 하지만 보손의 경우엔, 이론적으론 한 자리에 무한개의 보손이 존재할수 있고, 만약 보손입자의 총 갯수가 $N$개라고 가정해도 각 자리에 0부터 $N$까지의 입자들이 있을수 있기 때문에 $(N+1)^L$ 개의 경우의 수가 있습니다. 자리와 입자의 갯수가 늘어날수록 보손 시스템의 상태 갯수가 페르미온에 비해 훨씬 많다는걸 볼수 있죠.
저희 연구에선 보손 다체 국소화 (bosonic MBL)시스템을 효율적으로 계산할수 있는 방법을 구안했습니다. 방법은 꽤나 추상적이지만, 은유적으로 설명할수 있습니다. 상호작용이 없는 양자 시스템은 각 자리에 자기만의 주기를 가지고 있는 진자들을 모아놓은것이라고 생각할수 있는데요, 이때 각 진자는 자신의 추에게만 영향을 미치고, 자기만의 주기를 가지고 흔들거리며, 다른 자리에 있는 진자들에게 영향을 미치지 않습니다. 이 시스템에 입자간 상호작용을 추가했을때, 가장 대략적 근사로 상호작용은 각 진자의 주기만 변화를 주고, 나머지 요소는 바뀌지 않는다고 가정할수 있는데, 이 근사 방법을 물리학자들은 ‘푸엥카레-린드스테드 섭동 이론’ (Poincaré-Lindstedt perturbation theory) 이라고 합니다. 아주 간단한 근사임에도 불구하고, 저희는 이 방법이 다체 국소화(MBL) 시스템 고유의 특징적 현상을 보여주기에 충분하다는걸 확인했습니다.
다체 국소화 (MBL)시스템의 고유적 특성중 하나는 바로 상호작용으로 인해 정보가 느리게나마 전파된다는 점입니다. 위에 있는 커버 사진은 격자를 보여줍니다. 왼쪽은 상호작용이 없는 앤더슨 국소화 시스템의 격자이고, 오른쪽은 상호작용이 있는 다체 국소화 시스템의 격자입니다. x축은 공간이고, y축은 ‘로그 시간’ 인데, 위로 올라갈수록 간격이 급수함수적으로 증가하는 (예를들어 1, 10, 100, 등등) 시간 축 입니다. 밝은색은 정보가 전송되었다는것을 의미하고, 어두운색은 정보가 미치지 못했다는것을 의미합니다. 왼쪽은 상호작용이 없는 앤더슨 국소화(AL) 시스템, 오른쪽은 상호작용이 있는 다체 국소화(MBL) 시스템 입니다. 입자간 상호작용이 존재하기 때문에, 다체 국소화 시스템의 경우 아주 느리게나마 정보가 확산된다는것을 알수 있습니다.
이 연구에 대해서 더 궁금하시다면, PDF 버튼을 눌러 Physics Review B에 게시된 논문을 확인해 주시기 바랍니다.
초록 (클릭해 열고 닫을수 있습니다)
Recent experiments in quantum simulators have provided evidence for the Many-Body Localized (MBL) phase in 1D and 2D bosonic quantum matter. The theoretical study of such bosonic MBL, however, is a daunting task due to the unbounded nature of its Hilbert space. In this work, we introduce a method to compute the long-time real-time evolution of 1D and 2D bosonic systems in an MBL phase at strong disorder and weak interactions. We focus on local dynamical indicators that are able to distinguish an MBL phase from an Anderson localized phase. In particular, we consider the temporal fluctuations of local observables, the spatiotemporal behavior of two-time correlators and Out-Of-Time-Correlators (OTOCs). We show that these few-body observables can be computed with a computational effort that depends only polynomially on system size but is independent of the target time, by extending a recently proposed numerical method [Phys. Rev. B 99, 241114 (2019)] to mixed states and bosons. Our method also allows us to surrogate our numerical study with analytical considerations of the time-dependent behavior of the studied quantities.
