BSc Thesis - Coulomb branch of 𝓝 = 4, 𝑑 = 2 + 1 supersymmetric gauge field theories
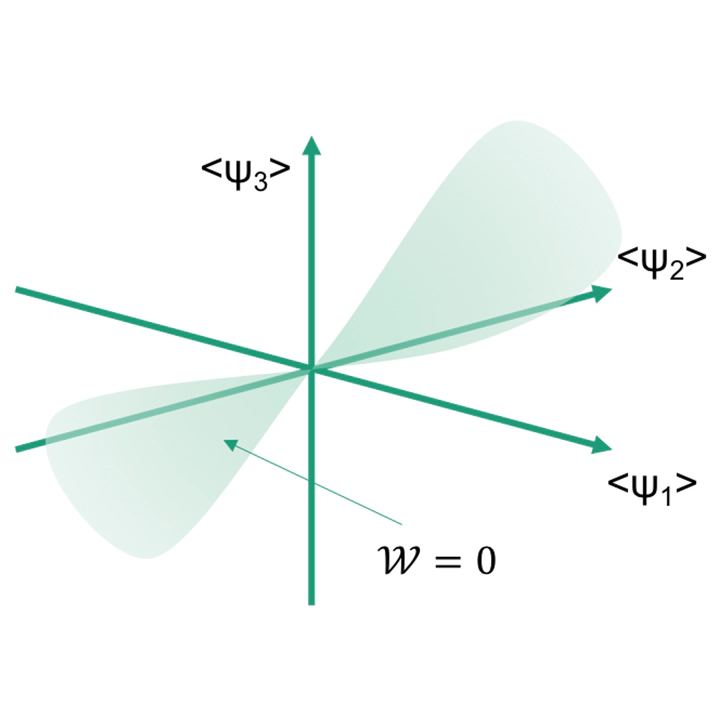 Moduli space, embedded in a space of scalar field vacuum expectation values. The mass of particles is determined by picking a point in this space.
Moduli space, embedded in a space of scalar field vacuum expectation values. The mass of particles is determined by picking a point in this space.
For the general public (click to open and close)
The famous Higgs mechanism, where a scalar (Higgs) field chooses one of the degenerate minima, gives particles their mass. In so-called supersymmetric gauge field theories, the space of degenerate minima is called the moduli space. Information about the moduli space is encoded in diagrams called ‘quiver diagrams’ and an algebraic series called the Hilbert series. We studied the structure of these moduli spaces for a particular set of these.
Abstract (click to open and close)
Moduli space of a gauge field theory is an abstract space of vacuum expectation values of scalar fields. It is of physical significance as a point in this space must be chosen before the masses of particles can be determined. For $\mathcal{N} = 4$, $d = 2 + 1$ supersymmetric gauge fields theories, whose information can be encoded in quiver diagrams, there are two branches in its moduli space: the Higgs branch and the Coulomb branch, where the latter can be calculated using the monopole formula. In this article, the Coulomb branch of $A_n$, $C_n$, $F_4$, $G_2$ Dynkin quivers and their affine counterparts were studied by calculating their Hilbert series using the monopole formula. In addition to confirming previous predictions, new implications on the choice of ungauging location (fixing one of the phases) were found, which we state as the ungauging hypothesis.